수학쟁이의 공부 이야기
말랑말랑 수학문제 #14 본문
<문제>
평면 위의 유한개의 점들의 집합 $S$ 의 임의의 서로 다른 두 점 $A, B$ 에 대하여 $AC = BC$ 가 되도록 하는 $S$ 의 점 $C$ 가 존재하면, $S$ 를 평행적이라 하자. $S$ 의 어떤 서로 다른 세 점 $A, B, C$ 에 대해서도 $PA = PB = PC$ 가 되도록 하는 $S$ 의 점 $P$ 가 존재하지 않으면, $S$ 를 비중심적이라 하자.
(a) 임의의 자연수 $n \geq 3$ 에 대하여 $n$ 개의 점으로 이루어진 평행적인 집합이 존재함을 보여라.
(b) $n$ 개의 점으로 이뤄진 평행적이고 비중심적인 집합이 존재하게 되는 자연수 $n \geq 3$ 을 모두 구하여라.
-----풀이 스포를 주의하세요-----
<풀이>
(a) 아무래도 이등변 삼각형이 되는 점을 찾는 것이다 보니 정 $n$ 각형을 떠올리는 것이 자연스럽다. $n$ 이 홀수인 경우부터 생각해보자.
case1) $n$ 이 홀수인 경우
원 위에 정 $n$ 각형을 그린다고 생각하자. 정 $n$ 각형에서 임의의 두 점 $(A, B)$ 를 잡게 되면 남은 점들은 총 $n-2$ 개가 존재하게 된다. 선분 $\overline{\rm AB}$ 를 기준으로 원은 두 영역으로 나눠지는데 $n-2$ 는 홀수이므로 두 영역 중 한 영역은 점이 홀수개가 존재하여 $AC = BC$ 가 되는 호의 중심에 위치하는 점 $C$ 가 존재한다.

case2) $n$ 이 짝수인 경우
$n$ 이 짝수인 경우 정 $n$ 각형으로는 잘 해결이 안 되어 다음 아이디어로 원을 떠올리게 되었다. 원 위에 어떻게 두 점을 잡아도 항상 중심이 수직 이등분선 위에 존재하기 때문에 이 점을 활용하여 문제를 풀어보겠다.
일단 백문이 불여일견이므로 내가 생각한 아이디어를 그림으로 먼저 그려보겠다.
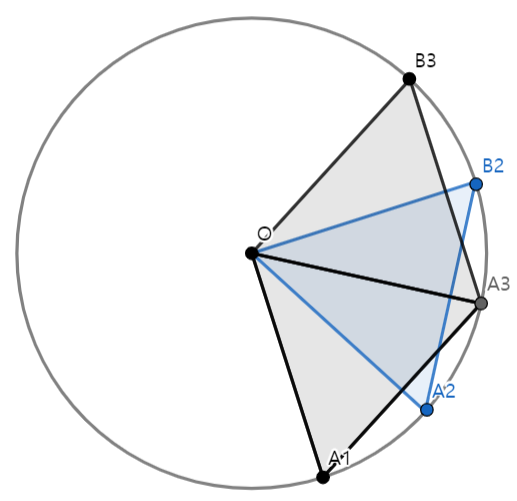
$n = 2k$ 라고 하고 원의 중심을 $O$ 라 하자. 점 $A_1, A_2, \cdots, A_k$ 를 $\angle{A_1OA_k} = 60^{\circ}$, $\angle{A_iOA_{i+1} = {\frac{60}{k-1}}^{\circ}}$ $(1\leq i \leq k-1)$ 을 만족하도록 원에 배열하자. 위 그림은 $k=3$ 일 때이다.
이러한 점들 $A_1, A_2, \cdots, A_k$ 를 $60^{\circ}$ 반시계방향으로 회전시켜 $A_1$ 과 $A_k$ 가 만나게 하자. 그러면 모든 점들이 원의 중심 $O$ 를 기준으로 $60^{\circ}$ 회전했으므로 $O$, 회전한 점과 회전된 점을 이어서 정삼각형을 만들 수 있다. 이렇게 잡으면 원 위에 임의의 두 점에 대해서는 점 $C$ 를 $O$ 로 잡으면 되고, $O$ 와 원 위에 임의의 한 점에 대해서는 점 $C$ 를 정삼각형이 되는 나머지 한 점으로 잡아주면 문제의 조건을 성립한다.
따라서 모든 $n \geq 3$ 인 자연수 $n$ 에 대해 평행적인 집합이 존재한다. $\blacksquare$
(b) (a) 에서 든 예시중 $n$ 이 홀수인 경우는 그 예시가 비중심적이므로 $n$ 이 홀수일 때는 (b) 조건을 만족한다.
이제 $n$ 이 짝수일 때 평행적이면서 비중심적일수는 없음을 보이겠다. 따라서 귀류법 사용을 위해 평행적이면서 비중심적이라고 가정하자. $n = 2k$ 라고 할 때 다음과 같은 쌍들을 더블카운팅 할 생각이다.
$$\{(A, B, C)| AC = BC \}$$
이 집합의 총개수를 $S$ 라 하자. $S$ 를 $(A, B)$ 기준으로 세어본다면 점 $C$ 가 임의의 $(A, B)$ 마다 하나씩 존재하므로 $S \geq \binom{2k}{2}$ 를 만족한다.
$S$ 를 $C$ 기준으로 세어본다면 비중심적이기 때문에 세 점 이상 같은 길이를 가질 수 없고 $n-1 = 2k-1$ 이 홀수이므로 최대 $k-1$ 개의 $(A, B)$ 쌍이 가능하다. 즉 $S \leq 2k(k-1)$ 이다.
$$k(2k-1) = \binom{2k}{2} \leq S \leq 2k(k-1)$$
첫 번째 항과 네 번째 항의 대소 관계에 의해 이 부등식이 모순이므로 따라서 $n$ 이 짝수일 때는 (b) 조건을 만족하지 않는다.
답) $n$ 이 홀수
'수학 문제 > 말랑말랑' 카테고리의 다른 글
| 말랑말랑 수학문제 #16 (0) | 2022.12.23 |
|---|---|
| 말랑말랑 수학문제 #15 (0) | 2022.12.22 |
| 말랑말랑 수학문제 #13 (0) | 2022.12.18 |
| 말랑말랑 수학문제 #12 (0) | 2022.12.18 |
| 말랑말랑 수학문제 #11 (0) | 2022.12.16 |

