목록선형변환 (3)
수학쟁이의 공부 이야기
2.3 Composition of linear transformations and matrix multiplication 두 linear transformation 의 합성 $U \circ T$ 를 편의상 $UT$ 로 표기하겠다. Theorem 2.9 $V,W,Z$ 가 field $F$ 위에서 정의된 vector space 이며 함수 $T : V \rightarrow W\,,\, U : W \rightarrow Z$ 가 linear 일 때 $UT : V \rightarrow Z$ 가 linear 이다. 증명) $x,y \in V \,,\, a\in F$ 에 대해 $$UT(ax+y) = U(T(ax+y)) = U(aT(x)+T(y)) = aU(T(x))+U(T(y)) = a(UT)(x)+UT(y)$$ 이므..
2.2 The matrix representation of a linear transformation $V$ 가 finite-dimensional vector space 일 때 ordered basis for $V$ 는 $V$ 의 basis 가 순서와 함께 고려되는 것을 말한다. 예를 들어 $\beta = \{e_1,e_2,e_3\}$ 와 $\gamma = \{e_2,e_1,e_3\}$ 둘 다 $F^3$ 의 basis 이지만 ordered basis 관점에선 $\beta \neq \gamma$ 이다. $F^n$ 에 대하여 $\{e_1,e_2,\cdots,e_n\}$ 은 standard ordered basis for $F^n$ 이라 하고 $P_n(F)$ 에 대하여 $\{1,x,x^2,\cdots,x^n\..
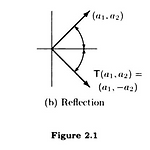 프리드버그 선형대수학 2.1단원 : 선형변환, 영공간, 치역의 정의
프리드버그 선형대수학 2.1단원 : 선형변환, 영공간, 치역의 정의
2.1 Linear transformations, null spaces, and ranges field $F$ 위에서 정의된 vector space $V,W$ 에 대해 함수 $T : V \rightarrow W$ 가 모든 $x,y \in V \,,\,$ $c \in F$ 에 대하여 $(a) \, T(x+y) = T(x) + T(y)$ $(b) \, T(cx) = cT(x)$ 다음의 조건을 만족한다면 $T$ 를 linear transformation from $V$ to $W$ 라 정의한다. field $F$ 가 유리수 집합인 경우 위의 $(a)$ 조건이 $(b)$ 조건을 포함하게 되지만 일반적인 경우 $(a)$ 와 $(b)$ 는 독립적이다. 예시를 살펴보면 다음과 같다. $1.$ $(a)$ 조건이 $(b..
